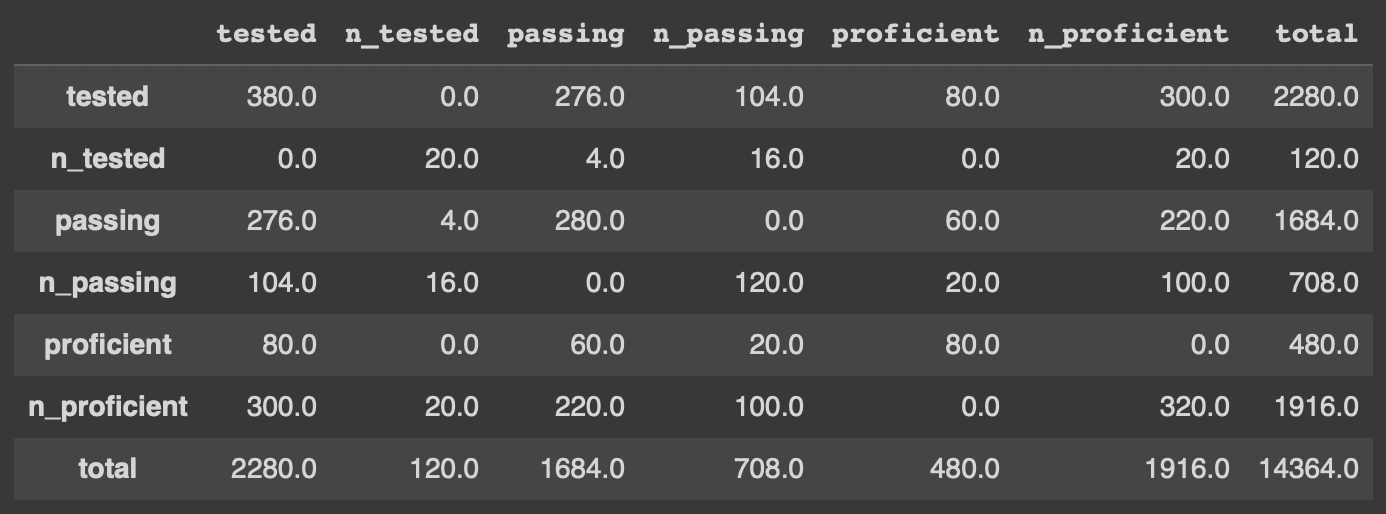
The essence of this project is finding a way to gauge teacher grading rigor. The EMD tool allows us to do that by comparing teachers’ grading distributions to the distribution of their students’ standardized test scores. If a teacher is grading rigorously, students who are unprepared for standardized testing should receive lower grades in their classes. If the grades a teacher gives in class actually reflect their students’ preparedness and performance on standardized tests, their distributions of grades and test scores will be quite similar and have only a small EMD between them. We can test these cross-metric distances for individual teachers using the EMD tool using the “Cross-comparison” metric option in the “Single-level EMD” tab.
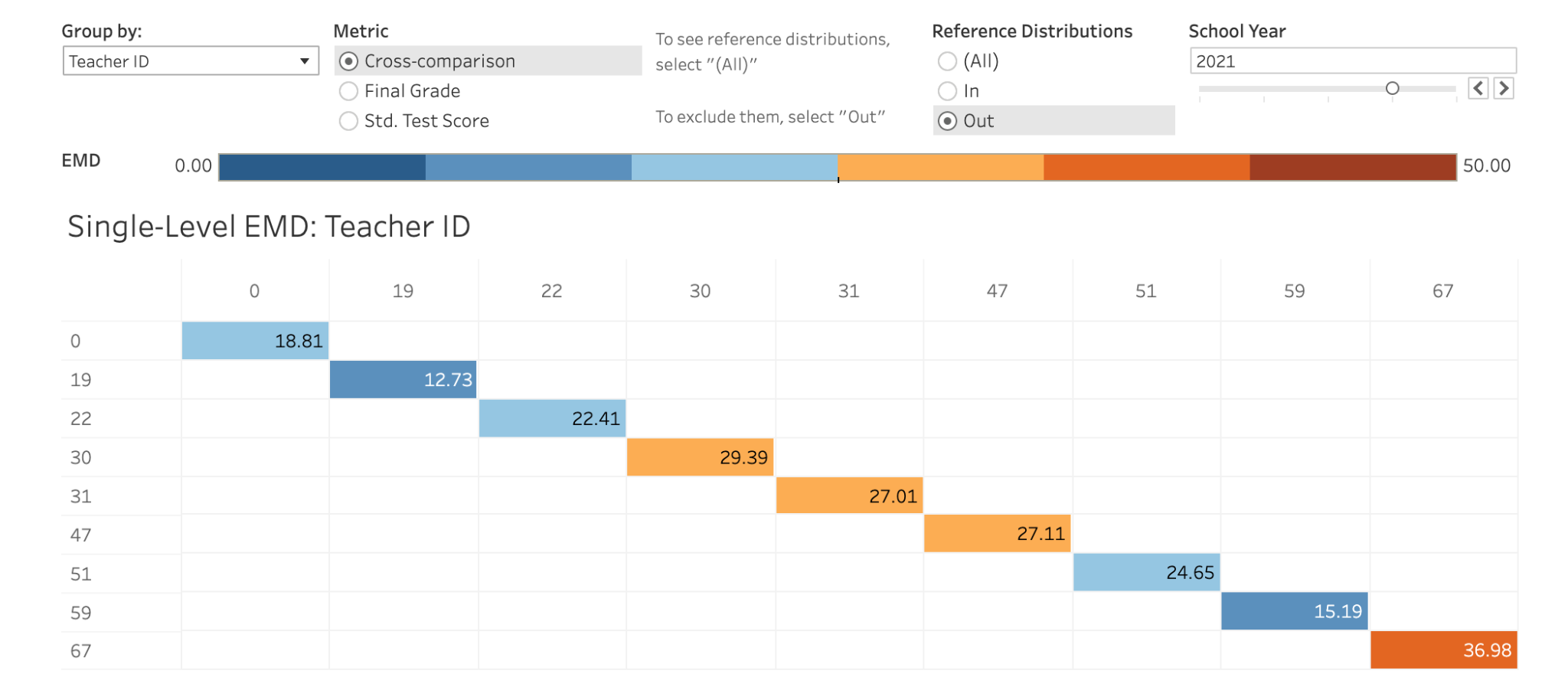
The visualization below shows the Earth Mover Distance between the distribution of final grades and the distribution of test scores for each teacher in the 2021 school year. I chose to exclude reference distributions from this view because comparing a C/300 average to itself will always yield an EMD of zero.
This view can teach us a few things. Most importantly, many of these numbers are in the top half of the range of EMDs in our data. That means that across all the comparisons we can make using this tool, comparing a teacher’s own grades to the test scores their students receive yields some of the highest EMDs possible. That doesn’t paint a good picture for grading rigor at this school.
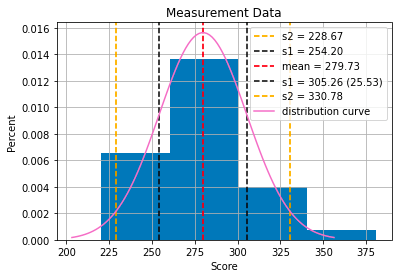
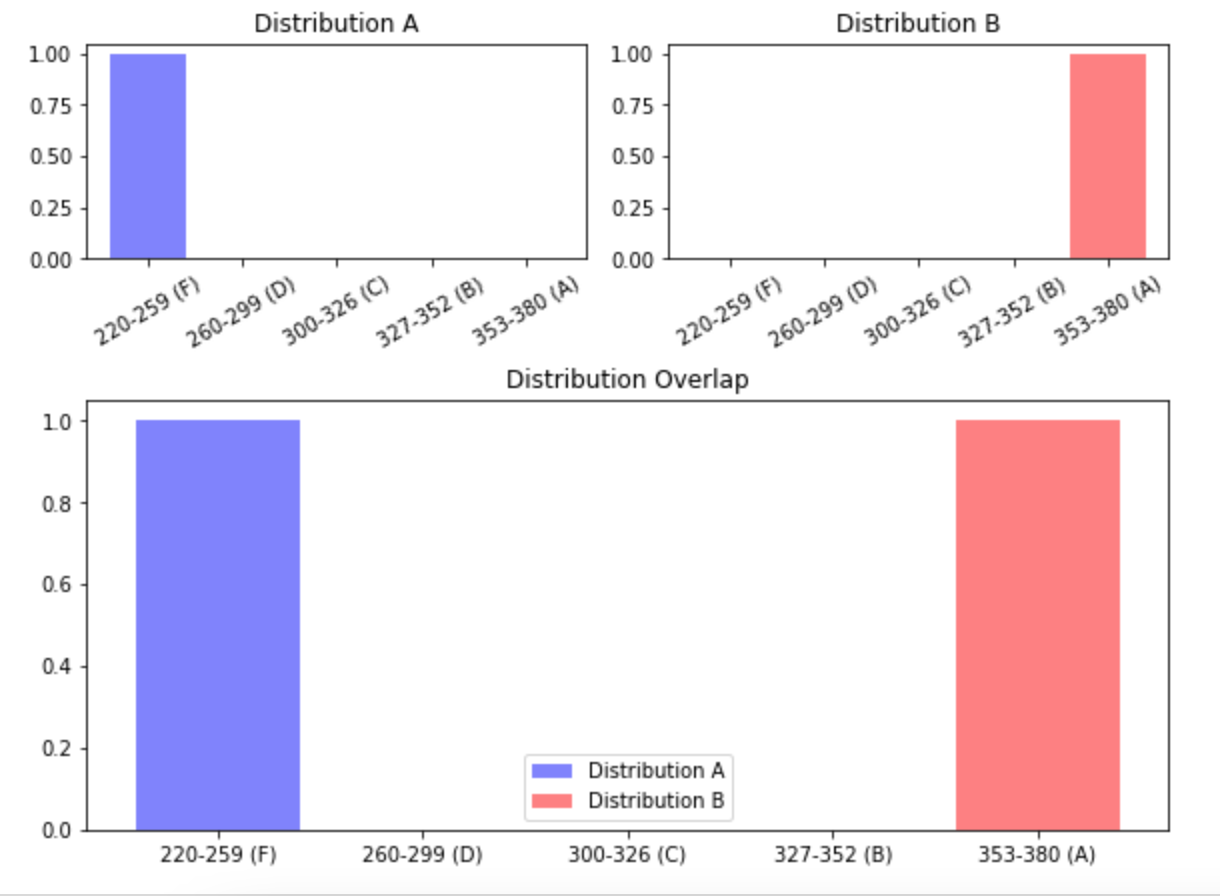
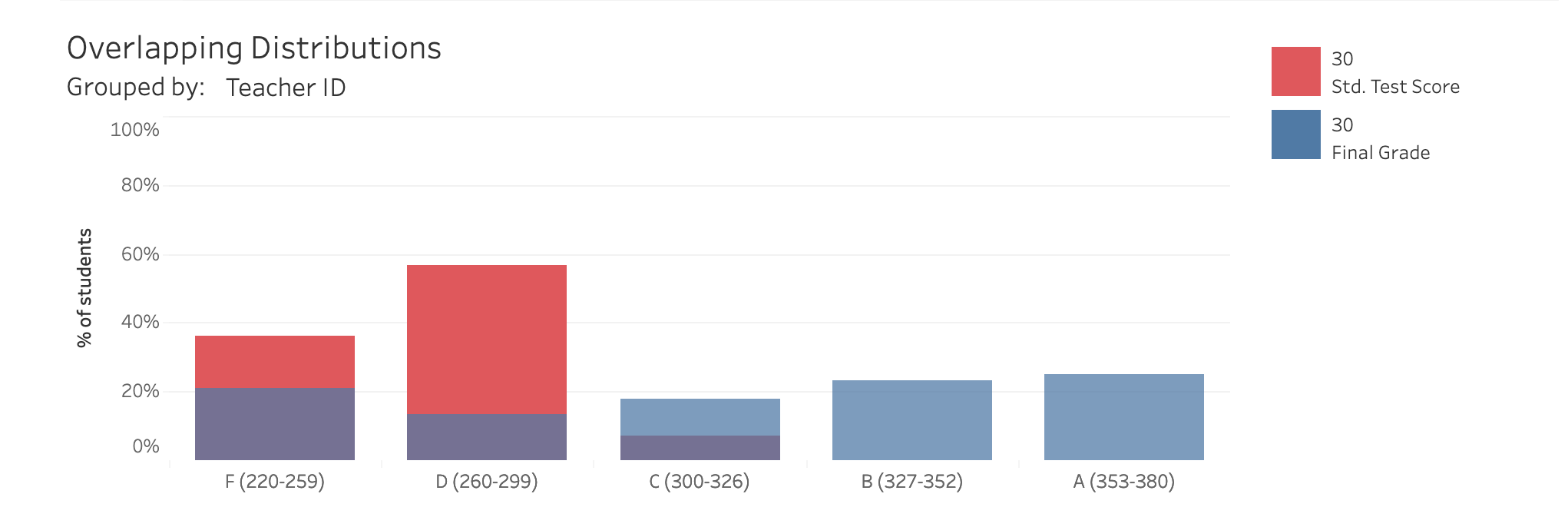
Let’s dive a little deeper and look at Teacher 30 specifically, who has one of the highest cross-metric EMD in this view. By clicking on the block that shows Teacher 30’s EMD in the matrix above, I can see the distributions of grades and test scores that are responsible for that EMD.
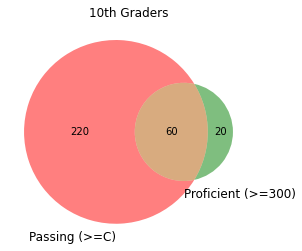
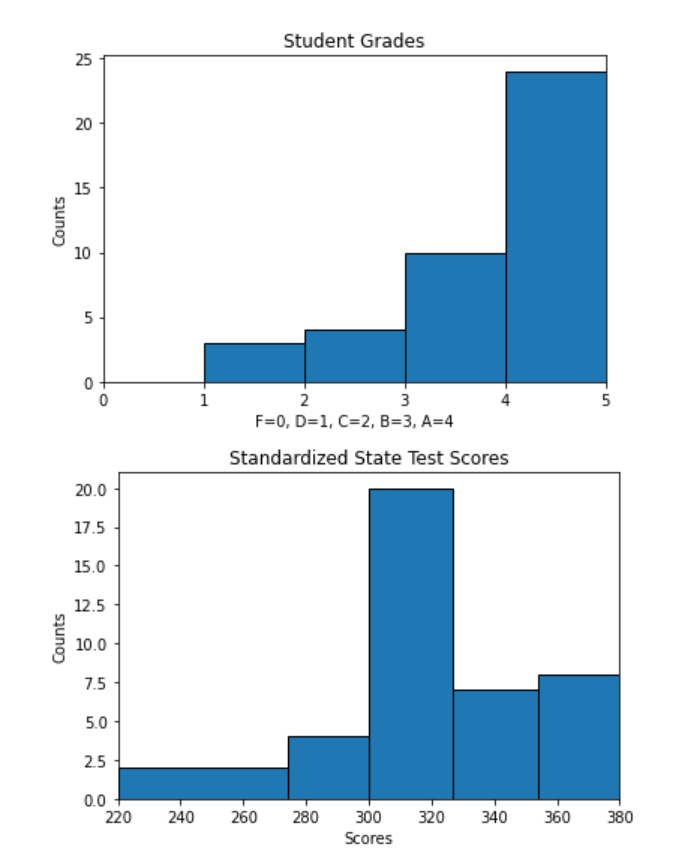
These distributions are, as expected, fairly different. The blue bars are of a fairly even height across the graph, meaning that Teacher 30 tends to assign around 20% of students their each letter grade. The red bars, on the other hand, are higher on the left side of the graph, revealing that those same students received failing grades on their 2021 standardized tests. The purple areas over C, D, and F grading regions signify areas where the two distributions overlap. In other words, Teacher 30 does give some students F’s and D’s on their final grades, but not nearly as many as would be appropriate if students’ final grades reflected their standardized test scores.
Overlapping distributions that look like this are a sign of grade inflation, which happens when a teacher rewards students with higher grades than their learning would actually reflect. If Teacher 30’s final grades reflected their students’ actual progress in learning the course material, the final grades would likely be much lower.
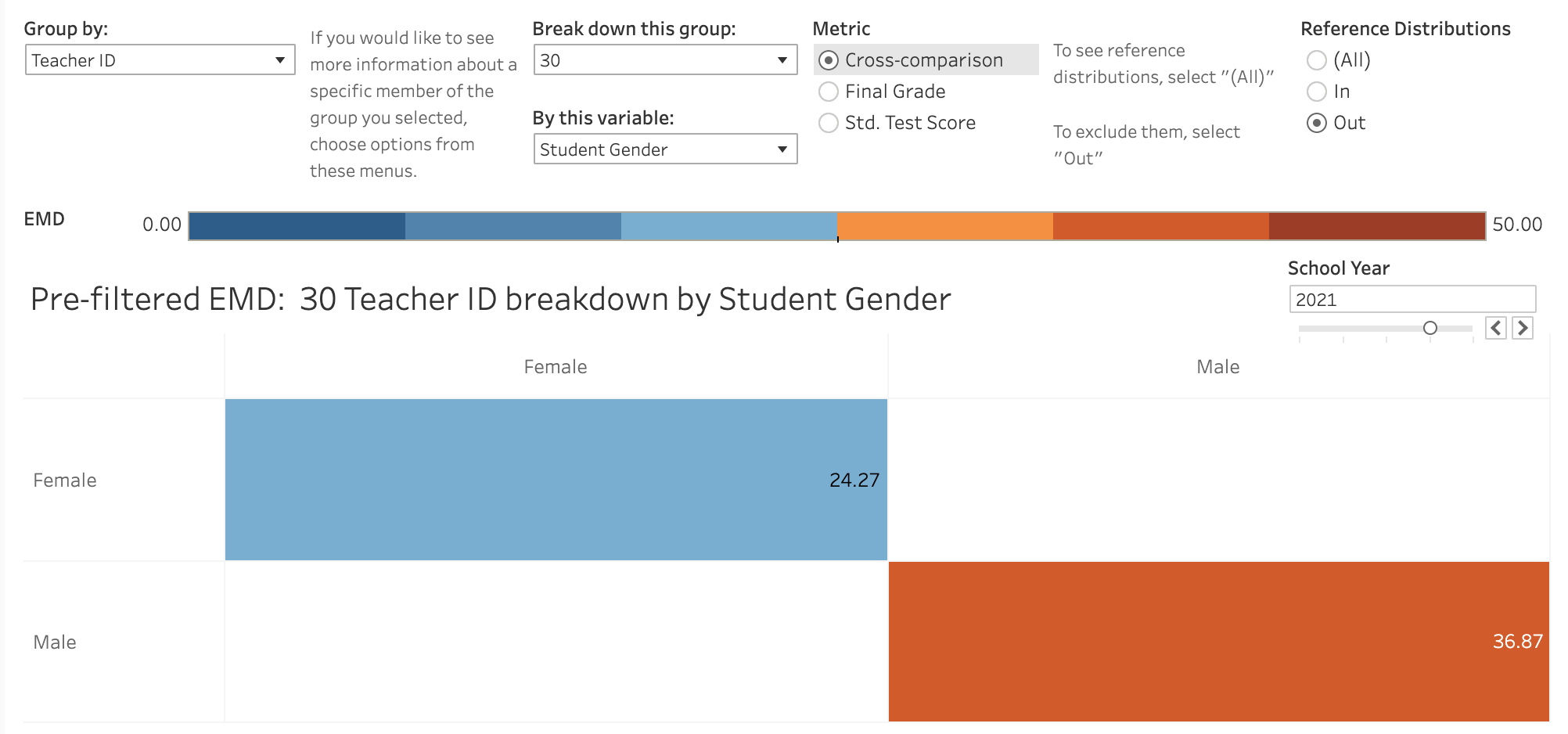
Since each one of these distributions is made up of individual students, it is worth investigating if any particular groups of students are disproportionately impacted by Teacher 30’s lack of grading rigor. To do this, we can use the prefiltered EMD tab to examine in more detail the breakdown of grades and standardized test scores within classes taught by Teacher 30.
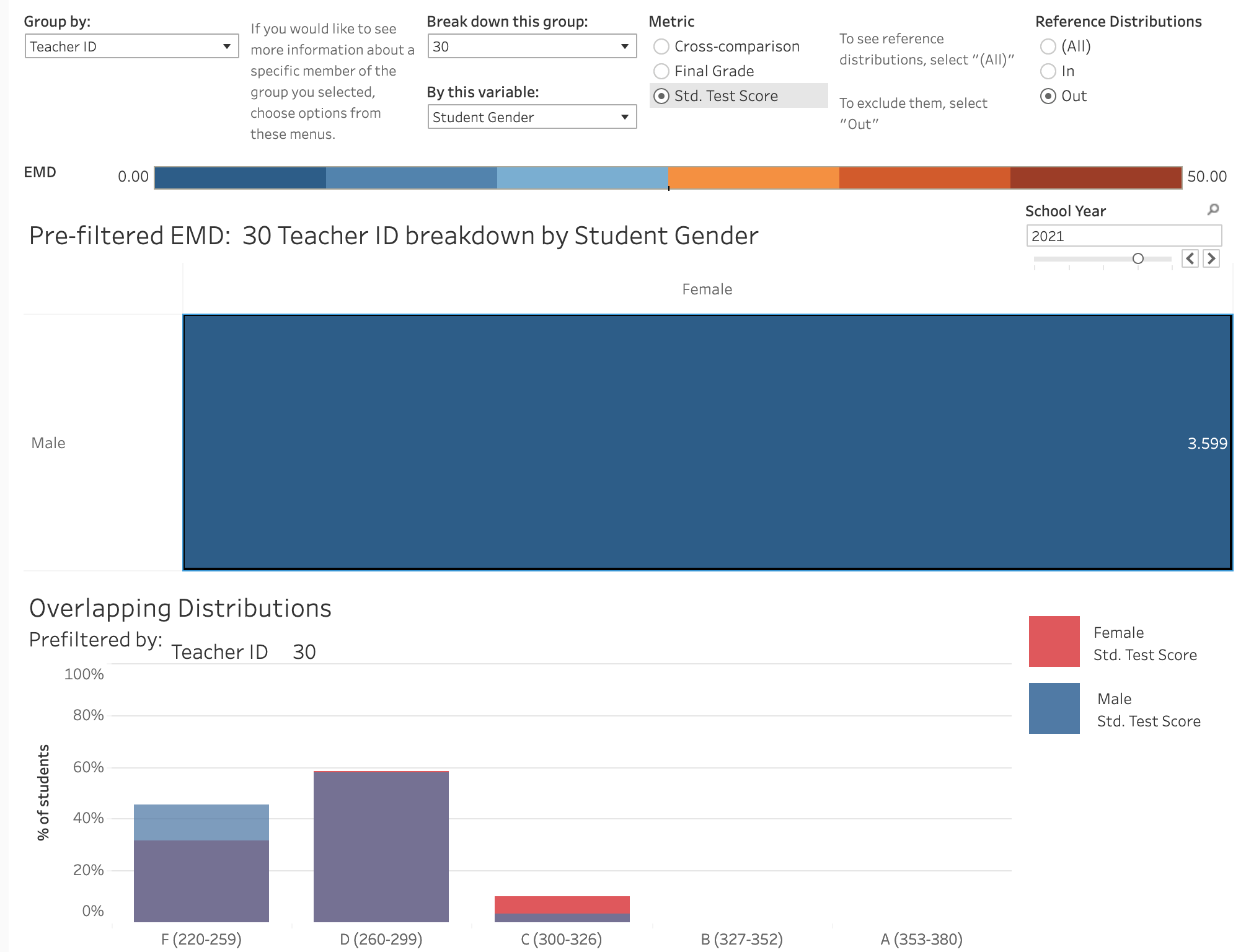
To do this, I move to the “Prefiltered-EMD” tab and choose to group by Teacher ID, then break down Teacher 30’s information by Student Gender. Since all of the data in this project comes from math classes and there is a dominant cultural narrative that girls are less naturally skilled at math than boys, examining differences in performance between male and female students is a reasonable place to start.
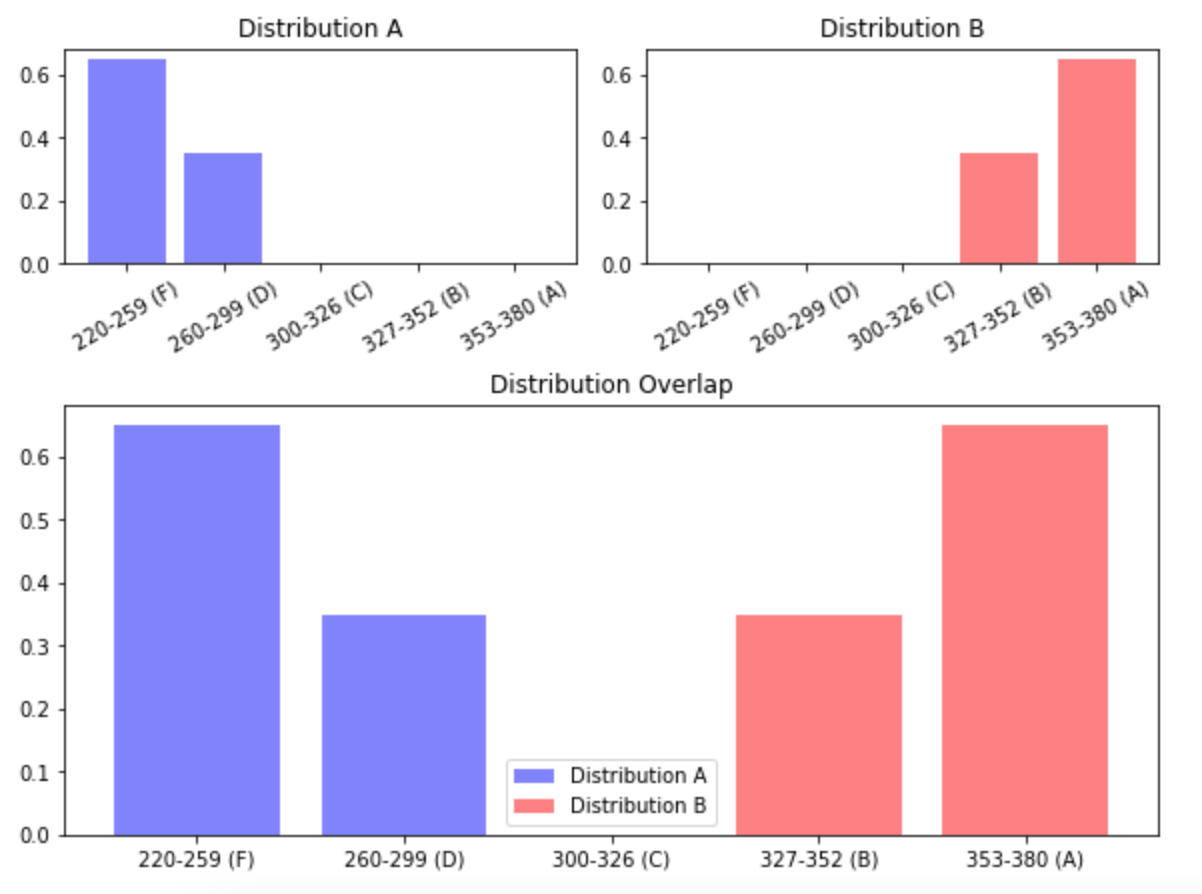
This view shows that the distributions of final grades between male and female students of Teacher 30 have an EMD of 9.295. Examining the overlapping distributions shows that this distance exists because male students tend to receive higher final grades than their female counterparts. Does that better performance in class translate to standardized test scores? If it did, I would expect to see a similar EMD between standardized test scores for these groups. To see if that is the case, I can change the metric to “Std. Test Scores” and keep all other settings the same.
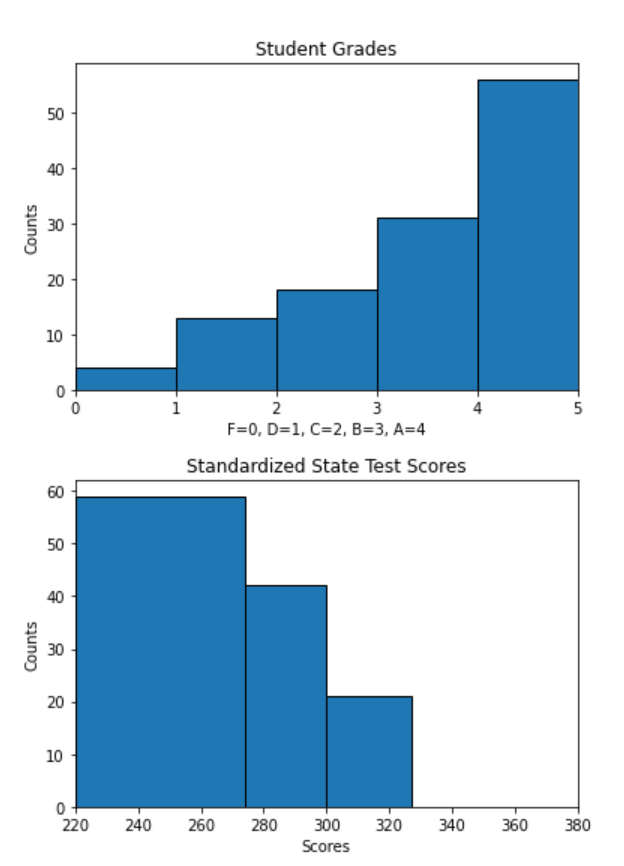
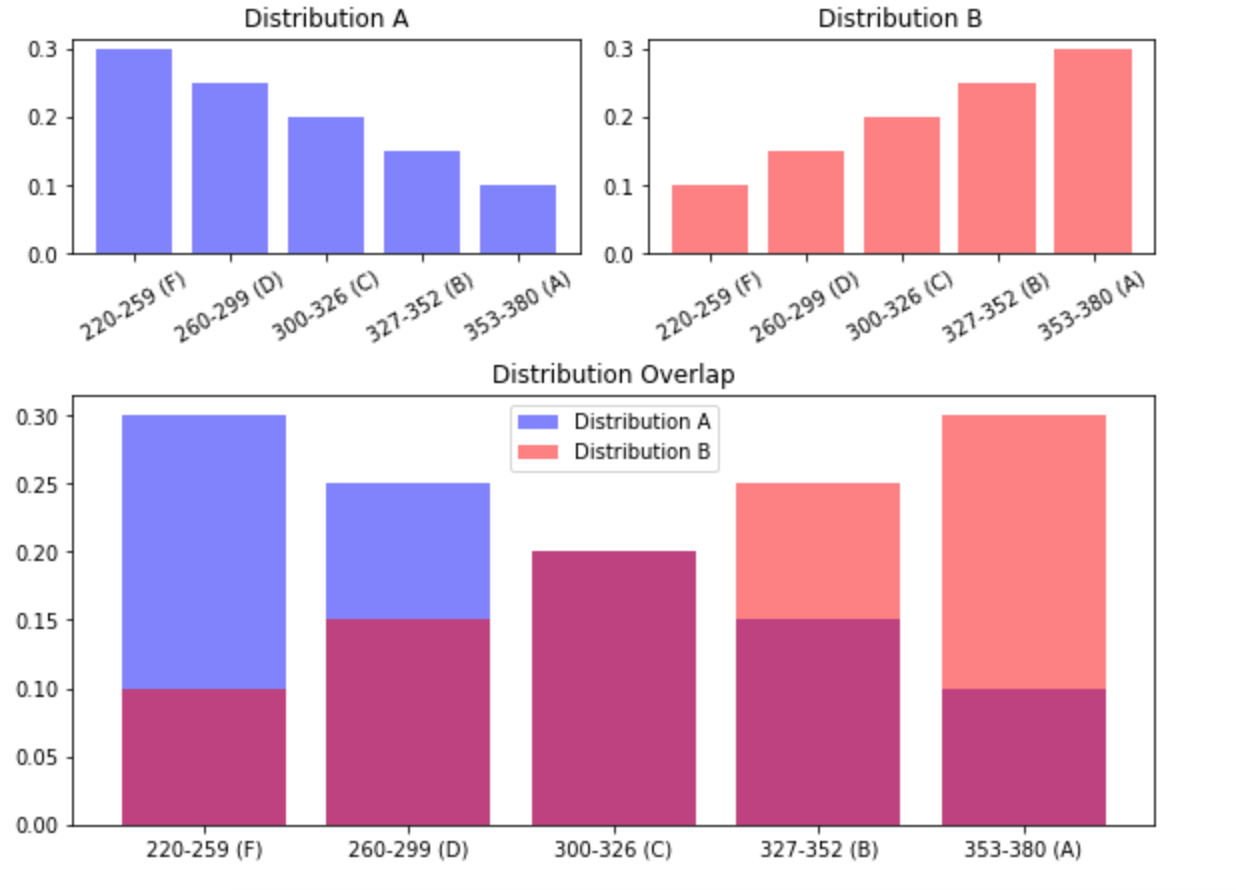
The distance between distributions of test scores for male and female students of Teacher 30 is not the same, but smaller than the distance between distributions of final grades - this means that students perform relatively similarly on standardized testing, even though their final grades would suggest male students have a better grasp of the material than females. In fact, females actually perform slightly better on standardized testing than males, despite receiving lower final grades. For a final view of this discrepancy in grading, I can view the cross-metric EMD for these groups by changing the metric to “cross-comparison” and keeping all other settings the same
This view confirms that there is a bigger distance between the distributions of final grades and test scores for males than there is for females. In other words, male students’ performance in class differs more from their performance on standardized tests. The previous views looking at each of those distributions individually let us know that this is because male students receive higher grades from Teacher 10, despite performing the same as their female counterparts on standardized tests. Female students have a lower EMD for this cross-comparison because their lower final grades more closely resemble their performance on standardized testing.
This analysis revealed that during the 2021 school year, Teacher 30 graded less rigorously than many of their colleagues. It also revealed that male students benefited the most from Teacher 30’s grade inflation habit. This information could inform an intervention in Teacher 30’s classes, from the introduction of a grading rubric to ensure that all students are reliably graded relative to their mastery of the subject, to targeting more attention to female students to get their grades up. In the future, the effectiveness of any changes can be gauged by comparing the EMDs in this analysis to those of future school years for the same groups - Can Teacher 30 reassess their grading or teaching strategies to get students’ grades in line with their standardized test performance?
.png)
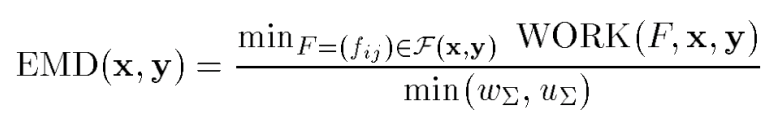
.png)
.png)
.png)
.png)